
さてさて。この画像を見て、「横の長方形」と「縦の長方形」のどちらが皆さんには長く見えるだろうか?
「ああ、錯覚(錯視)ね。」と気が付いた人も多いことだろうが、その通り。
そう。どちらも同じ長さだ。(垂直水平錯視)
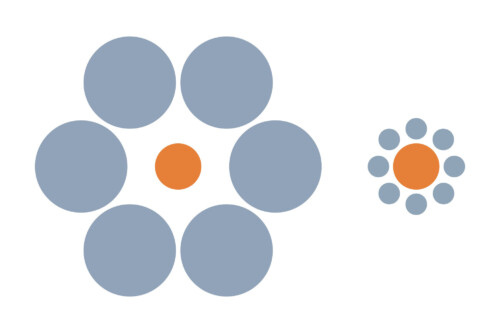
それでは、こちらのオレンジの円はどうだろう。(エビングハウス錯視)
う~ん。やはり僕には右が大きく見えるけど、もちろんこれも同じ大きさだ。
先週の小6の算数「拡大図と縮図」の問題で、このような図があった。
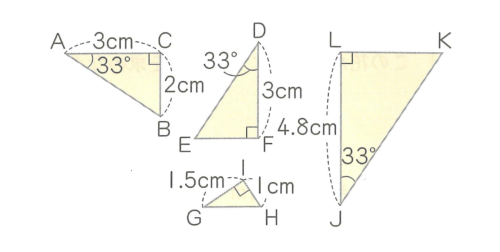
三角形ABCの拡大図と縮図の問題の問題だが、三角形DEFは三角形ABCと同じ大きさである。
しかし、錯覚(錯視)だとわかっていても、僕にはこの三角形DEFが、三角形ABCより大きく見えるのだ!
そこで、岡崎本校の6年生に聞いてみた。
宮「この図、三角形ABCより三角形DEFの方が大きく見える人、手をあげて~。」
結果は・・・
なんと全くの同数!!(あら、意外!!)
「え~!普通に同じ大きさにみえるケド」 🙄
「いや、ゼッタイ大きく見えるよ~」 😀
面白いのは、同じ大きさに見える生徒もたくさんいることだ。
う~ん、不思議だ。
さらに数日後、六名校で自習中(見せたのは休憩中です!)の中3のKさんに同じ図を見せたら、やはり大きく見えるとのこと。
そこに一緒にいた古里先生が、
「縦横もそうですが、三角形DEFは『33°』が外に書かれているのも、大きく見える原因じゃないでしょうか?」
と、冷静な分析。
なるほどね~。
じゃあ、「錯覚(錯視)」しない子がいるのはなぜだろう?
物体の大きさを、実際とは違って見せる
「エビングハウス錯視」は、どうやら
大人より子どもの方が錯視を起こしにくい
という以下のような研究結果があるそうだ。
錯視の起こしやすさに子どもと大人で差がある、というこの研究結果は、視覚を部分で捉えず、視覚全体を文脈として把握しようとする脳の能力がゆっくりと発達するものであることを示唆していると、スコットランドにあるスターリング大学の心理学者、Martin Doherty氏らの研究チームは述べている。
へ~。。。
脳の発達とかなんたらかんたら言ってるが、要するに…
『子どもの純粋な瞳(め)は騙されない』
ってことでいいのかな? 😀

※アイキャッチ画像は、「ミュラーリヤー錯視」といいます。






